Схема мироздания
Что объединяет древний орнамент, человеческое тело, элементарные частицы и земной шар? Симметрия. Именно она вдохновляет художников и служит нитью Ариадны физикам.

Аня и Боря играют: по очереди кладут на круглый стол монеты. На каждом ходу можно положить одну на любое свободное место, но сдвигать или убирать уже выложенные монеты нельзя. Проигрывает тот, кому некуда положить монету. Первый ходит Аня. Подберите для нее стратегию, позволяющую победить при любых ходах Бори. На первый взгляд, задача повергает в смятение. Пусть на столе умещается сто монет. Тогда у Ани есть сто вариантов первого хода, и для каждого из них у Бори будет 99 вариантов второго. То есть уже первые два хода дают 9900 сценариев! Полное же число возможных партий будет астрономическим. Как выбрать идеальную стратегию среди этих необозримых вариантов? Решение изящно: первым ходом Аня кладет монету в центр стола. Затем Боря делает свой ход, все равно какой. Следующим ходом Аня кладет монету строго симметрично монете Бори (относительно центра стола). Боря снова ходит, Аня симметрично повторяет его ход, и так далее. Аня раз и навсегда перекладывает на Борю бремя выбора. Если мальчик нашел место для своей монеты, то с противоположной стороны стола найдется точно такое же место для Аниной. А если не нашел, то проиграл, как рано или поздно и случится.
Лучший архиватор в мире
Рассмотрим еще одну задачу. В столовой ложке воды примерно 1024 молекул. Испарим ее, чтобы молекулы разлетелись. Сколько нужно чисел, чтобы описать положение всех этих молекул в пространстве? Положение каждой задается тремя координатами, итого нужно 3 × 1024 чисел. Это больше, чем стаканов воды в Мировом океане! Всей компьютерной памяти на планете не хватит, чтобы записать столько чисел.
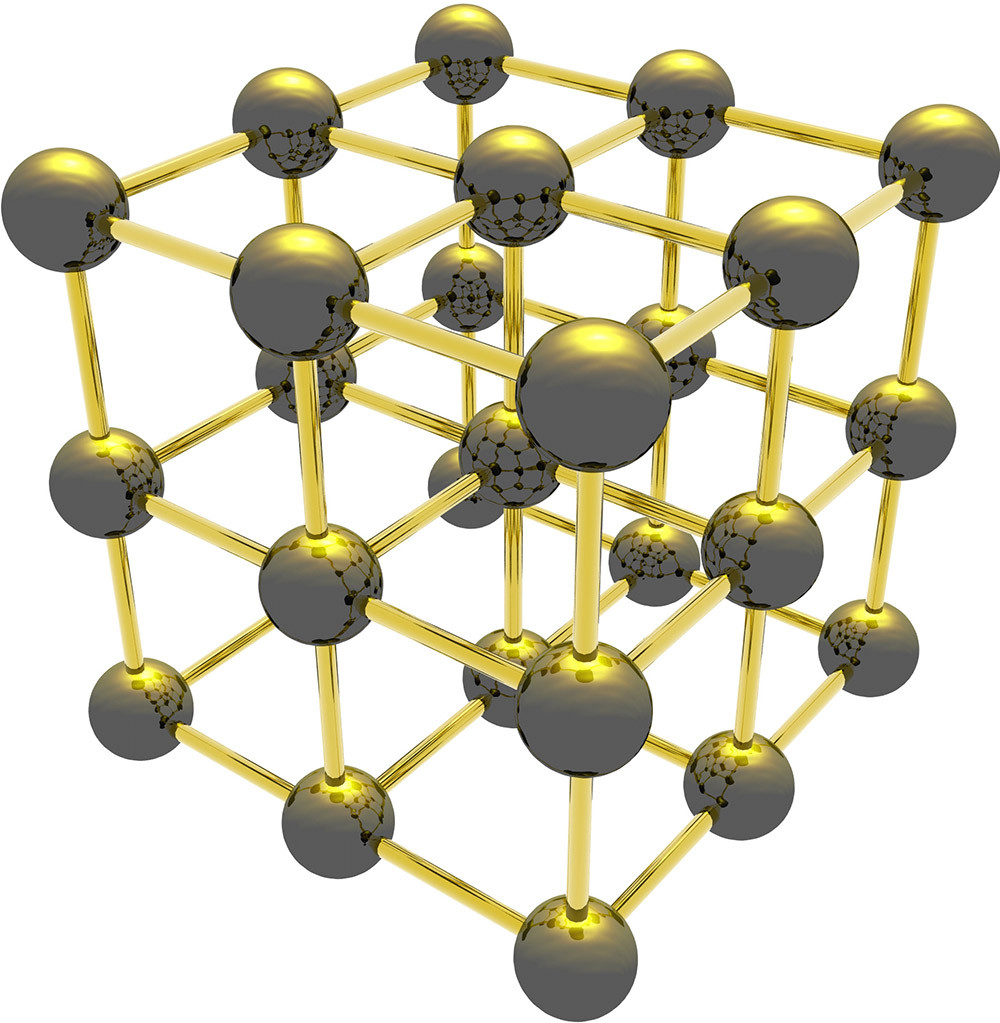
Теперь представим, что молекулы собраны в регулярную решетку из одинаковых кубов, где каждая молекула – вершина куба (на самом деле кубические кристаллические решетки встречаются крайне редко и уж точно не у льда). Сколько нужно чисел, чтобы описать положение всех 1024 молекул? Удивительно, но всего 12 чисел – чтобы задать центральный куб. Все остальные точно такие же кубы будут прилегать к нему гранями, обступая со всех сторон – и мы точно знаем, где будут их вершины.

В обеих задачах мы обошлись без формул и перебора необозримого количества вариантов. Более того, решения устойчивы к изменению условий. Идеальная стратегия не зависит от того, сто монет умещается на столе или сто тысяч. Она работает не только для круглого стола, но и, к примеру, для квадратного. Аналогично, если умножить количество молекул на миллиард или септиллион, их положение задаст тот же единственный центральный кубик. Экономия компьютерной памяти будет столь же впечатляющей, если заменить кубическую решетку на гексагональную, как у реального льда (хотя он и не образует столь идеальные кристаллы). Симметрия – мощнейший архиватор, упаковывающий неподъемное количество информации в компактные красивые схемы. Так координаты непредставимого числа молекул оказались заключены в параметры кубика.
Точка опоры
Что вообще такое симметрия? В обыденной речи: «что с одной стороны, то и с другой». Казалось бы, все понятно, но с одной стороны от чего именно? Ане ответ был ясен: от центра стола. Но подсунем игрокам стол в форме равностороннего треугольника. Аня кладет монету в центр, а Боря – в угол. Тут-то стратегия и дает сбой. «Отзеркалив» ход Бори от центра треугольника, Аня кладет монету не в угол, а на середину стороны. Все потому, что треугольник не обладает центральной симметрией (как называют это свойство математики). Легко понять, что это такое: начав с любой точки фигуры, идите в центр и считайте шаги. Миновав центр, идите столько же шагов, не сворачивая. Если фигура центрально симметрична, как круг или квадрат, точка финиша будет как две капли воды похожа на точку старта. Вышли из угла – придете в противоположный. А вот если центральной симметрии нет, финал может быть неожиданным. Значит ли это, что равносторонний треугольник – не симметричная фигура? В это трудно поверить, ведь «симметрия» означает «соразмерность». Что может быть соразмернее правильного треугольника? Разгадка проста: симметрия бывает не только центральной.
Рассеченные надвое
Какой симметрией обладают наши тела? Точно не центральной. Где ни ищи центр, на пути вверх от него мы встретим голову, а на пути вниз – совсем другие ландшафты. Наша левая половина зеркальное отражение правой. Может быть, провести вертикальную прямую через темя и считать от нее? Уже лучше, но считать от прямой можно не только влево-вправо, но и вперед-назад. Спереди – лицо, сзади – затылок. Снова не получается соответствия. Правильное решение – провести точно между глаз вертикальную плоскость. Где слева от плоскости ухо, там справа – другое ухо. То же касается глаз, ноздрей и т. п. А «вперед-назад» от этой плоскости считать нельзя: и вперед, и назад она уходит в бесконечность, рассекая нас надвое. Такая симметрия называется зеркальной.
