Вупи Голдберг в векторах: оцениваем размерность пространства лиц
Всякий раз, когда мы включаем телефон и глядим в камеру, ему приходится решать сложную задачу: понять, его ли хозяин сейчас пытается его включить. По сути, это один из самых близких нам сейчас примеров задачи распознавания образов. Ее можно сформулировать так: пусть у нас имеется большая библиотека фотографий лиц разных людей в разных ракурсах. Как по новой фотографии лица определить, принадлежит ли она кому-то из людей в библиотеке, и если да, то кому именно? Математик Денис Федосеев с мехмата МГУ и его коллеги попытались выяснить, какой размерности должно быть пространство признаков, которые позволят отличить Вупи Голдберг от Шона Коннери.
Чтобы решать задачу распознавания лиц при помощи компьютера, нужно сперва закодировать фотоснимки каким-то понятным компьютеру методом. Конечно, всякая картинка в памяти компьютера уже представлена некоторым кодом — например, многомерным вектором, где каждой его компоненте соответствует пиксель на картинке, а значение компоненты — это, например, представление цвета этого пикселя. Но у такой кодировки есть проблема: коды фотографий одного и того же человека, вообще говоря, не будут иметь между собой ничего общего. Потому что человек-то один, но сами картинки выглядят очень по-разному.
Решение этой проблемы пришло с развитием нейросетей. Не вдаваясь в подробности можно сказать, что нейросеть можно представлять как некий черный ящик, кодирующий фотографии «разумным образом»: так, что фотографии одного и того же человека получают хоть и разные, но в каком-то смысле похожие коды. Говоря более точно, нейросеть сопоставляет каждой фотографии точку в пространстве некоторой большой размерности, причем расстояния между точками, соответствующими одному человеку, достаточно малы по сравнению с размерами полученного облака точек, а точки, отвечающие разным людям, наоборот, более далеки друг от друга.
Лица в векторах
Итак, непонятные фотографии превращены в точки с учетом их принадлежности людям. Но теперь нужно разобраться, в каком смысле они «близки» или «далеки». В самом деле, рассмотрим простой пример. Пусть пространство, в котором живут полученные точки, двумерное — это плоскость. И пусть точки оказались размещены на спирали.
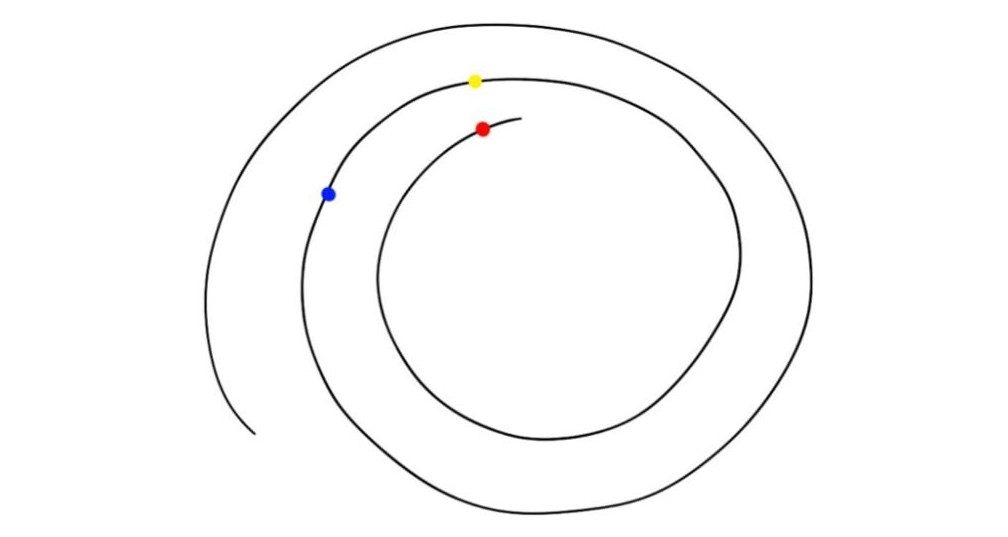
Расстояние на плоскости между красной и желтой точками — длина соединяющего их отрезка — меньше, чем расстояние между желтой и синей. Но если идти вдоль спирали, желтая точка окажется гораздо ближе к синей, чем к красной.
Значит, чтобы решить задачу распознавания образов, нужно понять, какую геометрию имеет множество точек, построенное нейросетью. Вопрос осложняется еще и тем, что объемлющее пространство, в котором живут точки, как правило имеет огромную размерность. Например, некоторые из стандартных в индустрии нейросетей (скажем, ResNet50 и ResNet100) работают с пространством размерности 512. Чтобы понять, насколько это необозримо, приведу пример: возьмем точку в 512-мерном пространстве и для каждой ее координаты скажем только, положительная она или отрицательная. Получим 2512 вариантов, что больше числа атомов в наблюдаемой части Вселенной. То есть для такой размерности даже простейшая попытка классифицировать точки по знаку координат обречена на провал.
К счастью, специалистами в этой науке давно сформулирована — и хотя и не доказана, но многократно экспериментально подтверждена, — так называемая «Гипотеза о многообразии». Она гласит, что точки, полученные из реального мира (например, как говорилось выше, из фотографий людей), сосредоточены в объемлющем пространстве вблизи некоторого многообразия существенно меньшей размерности. И геометрию этого-то многообразия и нужно определить, чтобы эффективно решать задачу распознавания.
Лоскутное одеяло
Многообразие — это, говоря неформально, многомерный «разумный» аналог кривой или поверхности. Пусть, например, у нас есть плоскость, двумерный объект. Если мы вырежем из нее маленький кусочек, получим так называемый двумерный диск. Разрешим себе изгибать этот диск — главное его не разрывать и не склеивать его точки. Теперь будем склеивать из таких изогнутых дисков «лоскутное одеяло». Полученный объект уже может быть устроен «хитрее» диска. Например, из двух изогнутых листов можно склеить сферу, которая на диск совсем не похожа. Это и есть неформальное описание устройства многообразия. В общем случае вместо двумерного диска — кусочка плоскости — нужно брать диски многомерные, кусочки многомерного пространства фиксированной размерности.
