Как икс стал неизвестным и к чему это привело

Товарищи учёные, доценты с кандидатами!
Замучились вы с иксами…
Владимир Высоцкий
На уроках математики в школе нас приучают обозначать неизвестную величину буквой x (на латыни она произносится как «икс»). Разумеется, не только ею, но эта буква используется чаще всего. Более того, икс перешагнул границы математики, став общепринятым символом неизвестного, неведомого, непонятного в науке и даже в массовой культуре. Достаточно вспомнить, что физик Конрад Рентген назвал открытое им излучение непонятной природы Х-лучами, а сериалу о загадочных и странных событиях его автор Крис Картер дал название «The X-Files» (в России сериал известен как «Секретные материалы»).
Почему же неизвестную величину принято обозначать именно буквой х? Попробуем разобраться в этом вопросе, попутно разоблачив несколько мифов, проникших даже в серьёзную литературу.
Но начнём мы с другого вопроса: а зачем математике вообще символьные, в том числе буквенные, обозначения? Не погрешив против истины, можно сказать, что именно символический язык сделал математику той могучей силой, какой мы её знаем сейчас, основой естественных и инженерных наук, в том числе физики и компьютерных технологий. Именно символика позволила представить сложные понятия, свойства изучаемых объектов и связывающие их законы в точной, однозначной и краткой форме. В свою очередь это привело к созданию методов и алгоритмов решения различных задач, а также вывода из известных истинных утверждений новых. Кроме того, правильно введённые обозначения помогают ставить задачи, понимать их суть, уменьшают умственные усилия на это и облегчают преобразования. Как заметил британский математик Альфред Уайтхед, удачное обозначение освобождает мозг от ненужной работы, тем самым позволяя ему сосредоточиться на более важных задачах.
К XVI веку, когда символы по-настоящему появились в науке, математика, по сути, ещё недалеко ушла от древних знаний полуторатысячелетней давности. Огромный рывок математики в XIX веке во многом обеспечен сформированной за предыдущие 300 лет системой обозначений. В древних математических трактатах всё записывали словами. Читая тексты, требовалось затратить немало усилий, чтобы понять, о чём идёт речь. Так что уже в те времена стало ясно, что формулировки надо упрощать, вводя символические обозначения. Первыми своё обозначение получили как раз неизвестные величины, которые требовалось найти в ходе решения математических задач, ведь известные значения можно просто записать цифрами, а вот как записать неизвестные?
Рассказ обо всей длинной и сложной истории формирования символов переменных займёт слишком много времени и места, поэтому речь пойдёт лишь о самых ключевых моментах.
Из глубины веков
Особые обозначения, причём только для неизвестных величин, использовали ещё вавилонские математики. Они создали великолепную шестидесятеричную систему счисления, что привело к развитию арифметики как целых, так и дробных чисел, а затем и алгебры. Решение линейных и квадратных уравнений и даже их систем достигло высокого уровня уже в эпоху Хаммурапи, правившего Вавилоном в 1793—1750 годах до н. э. Неизвестные величины вавилоняне называли «длина», «ширина» и «глубина», в точности так же, как мы сейчас называем их x, y и z. Любопытно, что произведение двух переменных они продолжали называть площадью, а произведение трёх переменных — объёмом. Это говорит о том, что первоначально алгебраические задачи пришли из геометрии. Позднее они уже могли быть с ней не связаны, хотя терминологию сохранили. Впрочем, иногда употребляли и отвлечённые названия вроде «множитель» и «обратное», соответствовавшие нашим х и у = 1/х.
Но где же здесь символика, спросит внимательный читатель, ведь это же просто слова? Всё дело в том, что в описываемое время в Вавилоне в ходу был аккадский язык, а слова «длина», «ширина» и т. д. изображались в текстах более древними шумерскими знаками, уже вышедшими из употребления. Так что эти знаки стали, по сути, математическими символами.
У древних египтян, не имевших позиционной системы счисления, с математикой дела обстояли хуже. Даже простейшие арифметические действия, особенно с дробями, для них представляли проблему. Однако обозначение для неизвестного, причём тоже на основе слова, было и у них. В этом значении они использовали понятие, означавшее кучу или количество. На письме оно изображалось иероглифами
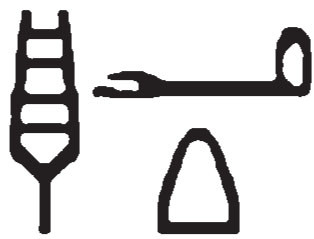
а в случае скорописи (иератического письма), как

В научной литературе его принято обозначать «aHa» или «h» (условно читается «аха», раньше писали также «хау»). Поэтому задачи, которые в наше время соответствуют линейным уравнениям, египтологами принято называть задачами аха. Таковыми, например, являются задачи 1, 19 и 25 из Московского математического папируса*, написанного около 1850 года до н. э., или задачи 24—30 из папируса Ахмеса**.
* Московский математический папирус, или Математический папирус Голенищева, — один из древнейших известных математических текстов, написан около 1850 года до н. э. Хранится в Музее изобразительных искусств им. А. С. Пушкина в Москве. Первым его владельцем был один из основателей русской египтологии Владимир Семёнович Голенищев.
** Папирус Ахмеса, или папирус Ринда, — древнеегипетское учебное руководство по арифметике и геометрии, представляющее собой сборник задач с решениями. Вариант, хранящийся в Британском музее, переписан около 1550 года до н. э.
В качестве примера приведём задачу № 26 из папируса Ахмеса, которая формулируется примерно так: «aHa и её четвёртая часть вместе дают 15. Чему равно aHa?». Это эквивалентно современному уравнению
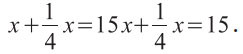
К такой идее приходили, видимо, все древние цивилизации. Решение линейных уравнений и их систем в первом тысячелетии до нашей эры, а, возможно, даже раньше, освоили и математики Древнего Китая. Об этом свидетельствует энциклопедический трактат «Математика в девяти книгах» («Цзю чжан суаньшу»), окончательно отредактированный во II веке до н. э. В нём неизвестную величину обозначали иероглифом «тянь-юань» — «небесный элемент», «небо». Для других неизвестных китайцы использовали специальные позиционные методы, а также иероглифы, обозначающие слова «земля», «человек» и «вещь».
К сожалению, древние греки не унаследовали у вавилонян ни позиционную систему счисления, ни алгебру, предпочитая геометрические рассуждения, а потому не интересовались и алгебраическими символами. Это сильно затормозило развитие математики в Европе. Исключение составлял лишь гениальный Диофант Александрийский (III век), недаром термин диофантовы уравнения дожил до наших дней. Именно у него впервые появляется буквенная символика. Неизвестную величину Диофант называл «числом» (άριθμός) и обозначал буквой ς. Ввёл он специальные знаки и для степеней неизвестного, вплоть до шестой. Например, квадрат неизвестного он обозначил символом ΔΥ (от δύναμις— «степень»), а куб — ΚΥ (от κύβος — «куб»). Правда, некоторые исследователи предполагают, что это были знаки для скорописи, а не алгебраические символы. (В наше время подобную запись текста с помощью знаков и сокращений называют стенографией.) Пусть даже и так. Главное, буква ς выполняла у него почти ту же функцию, что и наш x.

Идеи Диофанта не нашли последователей ни в его время, ни в последующие столетия. В средневековой Европе о нём надолго забыли. Однако ему, как и многим другим древнегреческим учёным, повезло, что их труды сохранились в арабском мире. В 1572 году в Италии «Арифметика» Диофанта была переведена с арабского на латынь. Диофант, фигурально говоря, триумфально вернулся в Европу. Теперь его труд оказал большое влияние на математиков, в частности, на основоположника современной символической алгебры Франсуа Виета (разговор о его трудах ещё впереди). Кстати, в 1637 году Пьер Ферма записал формулировку своей великой теоремы именно на полях «Арифметики» Диофанта.
