Гало-орбита: в ожидании полета человека
Новый шаг человека в дальний космос связан и с шагом в пилотируемой космонавтике — освоением принципиально нового типа орбит. Для полетов людей эти орбиты никогда не использовались. Но они оказались наиболее подходящими для одновременного решения целого ряда ключевых задач. И полет человека по ним готовится сегодня практически.

Гравитация планеты изгибает своим полем путь объекта, пролетающего рядом мимо нее. Эту кривую Иоганн Кеплер назвал орбитой (от латинского слова orbita — «колея», «путь»). Поле тяготения — это распределенные в пространстве вокруг планеты гравитационные ускорения, направленные к центру поля, растущие ближе к нему и слабеющие с удалением. По законам Кеплера объекты, не покидающие поля тяготения планеты и не испытывающие других сил, кружатся вокруг центра поля по эллипсам (и окружностям, их частный случай). Это спутники планеты. Их бег в гравитационном поле похож на воронку водоворота: чем ближе к центру, тем быстрее.
Основа космической баллистики
Эллипсы устойчивы. Без других сил, кроме поля обращения, форма и размеры кеплерова эллипса не меняются, как и его положение в пространстве, и полет по нему. Спутник проходит за оборот все те же точки орбиты с теми же скоростями в них. Не зря Кеплер назвал это «колея». Меняется орбита лишь другой силой к спутнику либо из-за несферичности поля тяготения. Один из двух своих «центров», фокусов, эллипс держит в центре гравитационного поля, совмещая в одной точке обоих. Третьим в нее подсаживается барицентр — центр обращения спутника.
По эллипсам движутся спутники Солнца — планеты, астероиды, кометы, метеорные тела и потоки. По кеплеровым орбитам летят спутники планет в местных гравитационных полях. Человек рассчитал, а затем освоил эллиптические орбиты. Иоганн Кеплер определил эллипсы (1609), Вальтер Гоман дал переход с одного эллипса на другой (1925), Сергей Королев запустил аппарат (1957). Околоземный космос населяют более 5 тыс. искусственных спутников на эллиптических (круговых) орбитах, решая десятки тысяч задач. Их число стремительно растет. По эллипсам спутника Солнца аппараты летят, покинув Землю, в ходе перелетов к другим телам и полетным целям. Можно уверенно сказать, что кеплеровы эллипсы — основа сегодняшней орбитальной баллистики.
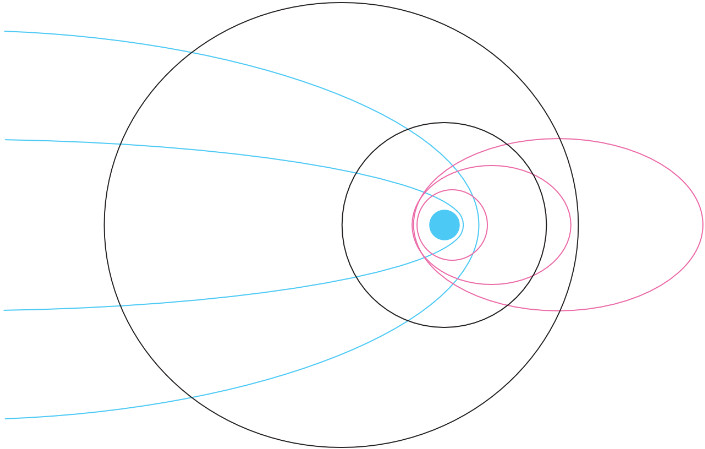
Удаляясь от Земли, аппарат может оказаться в гравитационно другой ситуации. Вместо одного тяготения на него существенно действуют сразу два — разных и из разных точек. Вместо гравитационной системы двух тел — одной планеты с центральным полем тяготения и аппарата — он попадает в систему трех тел: себя и двух больших масс, создающих свою гравитационную систему. Например, Солнце и Земля, Земля и Луна.
Жозеф Луи Лагранж ровно 250 лет назад в математических решениях упрощенной задачи трех тел нашел у такой системы пять особых точек, названных точками Лагран жа, или L. Их смысл — неизменность положения относительно тел. Это угловая неподвижность. У системы двух тел, Земли и аппарата, таких точек бесконечно много — вся геостационарная орбита. А в системе трех тел (двух тяготеющих и аппарата) нет такой стационарной орбиты. Она вырождается во всего лишь пять точек. Они неподвижны относительно меньшего тяжелого тела во вращающейся системе координат (с главным тяжелым телом в центре). И вместе с меньшим телом обращаются синхронно с ним вокруг большего, описывая вокруг него орбиты. Три из этих точек — L5, L4 и L3 — лежат вдали от тяжелых тел, почти на орбите меньшего тела (но не близко к нему). Точка L3 системы Солнце—Земля расположена напротив Земли за Солнцем. Точки L4 и L5 отходят от нее вправо и влево на треть орбиты Земли. Они лежат вблизи орбиты, в 150 млн км от Солнца и Земли, образуя с ними равнобедренный треугольник. Первые точки, L1 и L2, лежат близко к меньшему телу — они ценнее практически.
В системе Солнце—Земля L1 лежит в 1,5 млн км от Земли прямо к Солнцу. Это 1% расстояния от Земли до Солнца. Ближе к Солнцу — там на 2% сильнее ускорение тяготения Солнца, и тела бегут быстрее, чем на земной орбите. Но в L1 Земля тоже тянет к себе, вверх, уменьшая действие солнечной хватки ровно на те же 2%. Итоговое гравитационное ускорение здесь выходит как на орбите Земли. Тогда будет и такое же обращение — тело в L1 идет синхронно с Землей, весь год неподвижно для Земли.
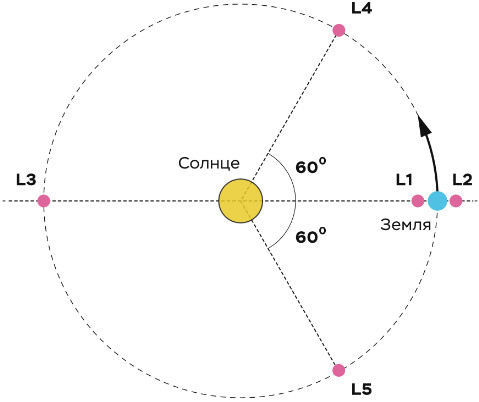
В обратном Солнцу направлении, в 1,5 млн км от Земли лежит точка L2. Здесь гравитация Солнца слабее, чем на орбите Земли, на те же 2%. А родная планета добавляет ровно столько же своей гравитации. В итоге тяготение в L2 такое же, как на земной орбите, а значит, и период обращения — ровно год, и неподвижность относительно Земли.
В точки L системы Солнце—Земля запущены аппараты. Ближе к Солнцу в L1 разместились солнечные обсерватории SOHO, ASE, DISCOVER, исследовательские WIND и Genesis. В точку L2 дальше от Солнца отправлены телескопы Gaia, «Гершель», «Планк», знаменитый «Джеймс Уэбб», российский «Спектр-РГ» и другие аппараты. У точек L1 и L2 (и у L3 тоже) есть еще особенность: пребывание в них неустойчиво. При мелком сдвиге из этих точек нет автоматической силы, возвращающей обратно. Наоборот, объект будет медленно удаляться. Поэтому ни один аппарат не находится точно в точках Лагранжа. Ведь в реальности и сами точки немного сдвигаются за один оборот Земли. Орбита Земли не круговая, а эллиптическая. Расстояние до Солнца «гуляет» за год на 5 млн км (или 3,3%, не так и мало!), меняя и удаление точек Лагранжа. В итоге аппараты не стоят в самих L, а движутся вокруг. Причем особым образом.
Система координат с неподвижными точками L вместе с Землей вращается вокруг Солнца. Это рождает в ней две силы инерционной природы — центробежную и силу Кориолиса. Они добавляются к тяготениям тел во всем пространстве. Силовой квартет тянет и аппарат, летящий около точки Лагранжа. В ряде сочетаний скорости, направления и положения аппарата четверка сил гнет его путь в петлю вокруг точки Лагранжа. Аппарат чертит вокруг L кривую — орбиту. Но не такую, как четко определенные кеплеровы эллипсы.
