Геометрия в стиле да Винчи

Один историк искусства как-то посетовал на то, что Леонардо да Винчи тратил талант и время на многочисленные рисунки, увлёкшись своей «геометрической игрой». Речь шла о задаче на преобразование криволинейных фигур в многоугольники, надолго поглотившей внимание художника. Леонардо с таким мнением вряд ли согласился бы: игра эта была интеллектуальной, усилия оказались ненапрасными, а на коллекцию рисунков имелись кое-какие планы. И вообще, преобразование фигур и тел стало главной темой его математических исследований.
Квадратура луночек
Как геометр и как художник Леонардо да Винчи с увлечением изучал плоские фигуры, ограниченные дугами окружностей. Страницы его записных книжек пестрят чертежами, где изображены луночки, «лепестки», сегменты и прочие криволинейные фигуры вкупе с кругами и многоугольниками, их образующими. Одни рисунки выполнены от руки, другие с помощью инструментов. Некоторые из них напоминают цветочные узоры и используются как элементы орнамента. Годами Леонардо пытался преобразовать одни фигуры в другие и придумывал новые, всё более сложные их комбинации, этакие импровизации на тему пленившей его задачи. Даже собирался написать книгу «О геометрической игре», посвящённую приёмам, которые, как он считал, обеспечат бесконечное разнообразие квадратур криволинейных фигур. Иными словами, для каждой из них можно будет построить многоугольник такой же площади. Леонардо да Винчи — один из первых европейских учёных, кто заинтересовался этой проблемой.

Долгое время его занимали круговые луночки — серповидные фигуры, ограниченные дугами двух окружностей. Их рассматривали ещё античные учёные, пытаясь осуществить квадратуру круга «по частям». В V веке до н. э. греческий геометр Гиппократ Хиосский, автор первых «Начал» (до нас труд не дошёл), открыл три вида квадрируемых луночек, позже названных его именем. Это были первые криволинейные фигуры, которые удалось преобразовать в равновеликие им многоугольники. К главной цели Гиппократ ничуть не приблизился, а математикам последующих поколений досталась ещё одна занятная тема для исследований.
В эпоху Возрождения квадратура луночек рассматривалась уже как самостоятельная задача, а вопрос об их количестве оставался открытым. Из современников да Винчи её касался итальянский гуманист Джорджо Валла. В 1501 году в Венеции вышла составленная им энциклопедия разных наук, и одна из статей рассказывала о гиппократовых луночках. Очевидно, из этой книги художник и узнал о знаменитой задаче древности.
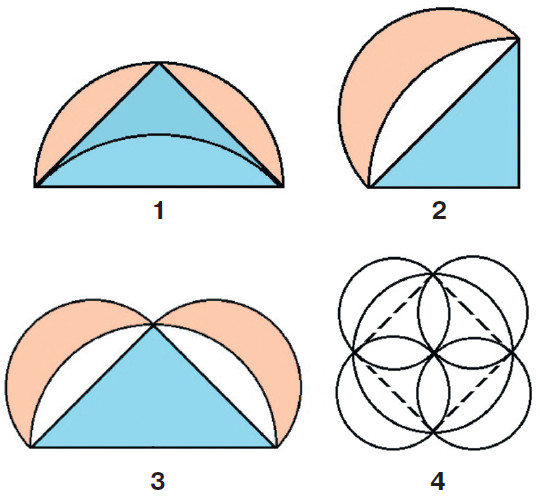
Леонардо экспериментировал с самой простой луночкой, у которой внешний обвод — полуокружность, а внутренний — четверть окружности. Её можно получить так: вписать в полукруг равнобедренный треугольник и внутри него на гипотенузе построить сегмент, подобный сегментам, отсекаемым катетами. Другой способ построения ещё проще. Нужно взять четверть круга и вне его на хорде, соединяющей концы радиусов, описать как на диаметре полуокружность. Нетрудно убедиться, что в обоих случаях луночка и треугольник равновелики. Гиппократу приписывают доказательство теоремы: сумма площадей двух луночек, примыкающих к катетам равнобедренного прямоугольного треугольника, равна площади этого треугольника. Интересно, что в конце XIX века один историк математики увязал происхождение квадратуры этой луночки с распространённым орнаментом из пяти пересекающихся кругов. В этом узоре четыре внешние луночки равновелики квадрату, вписанному в большой круг. Такую же и подобные ей конфигурации детально изучал и Леонардо-геометр.
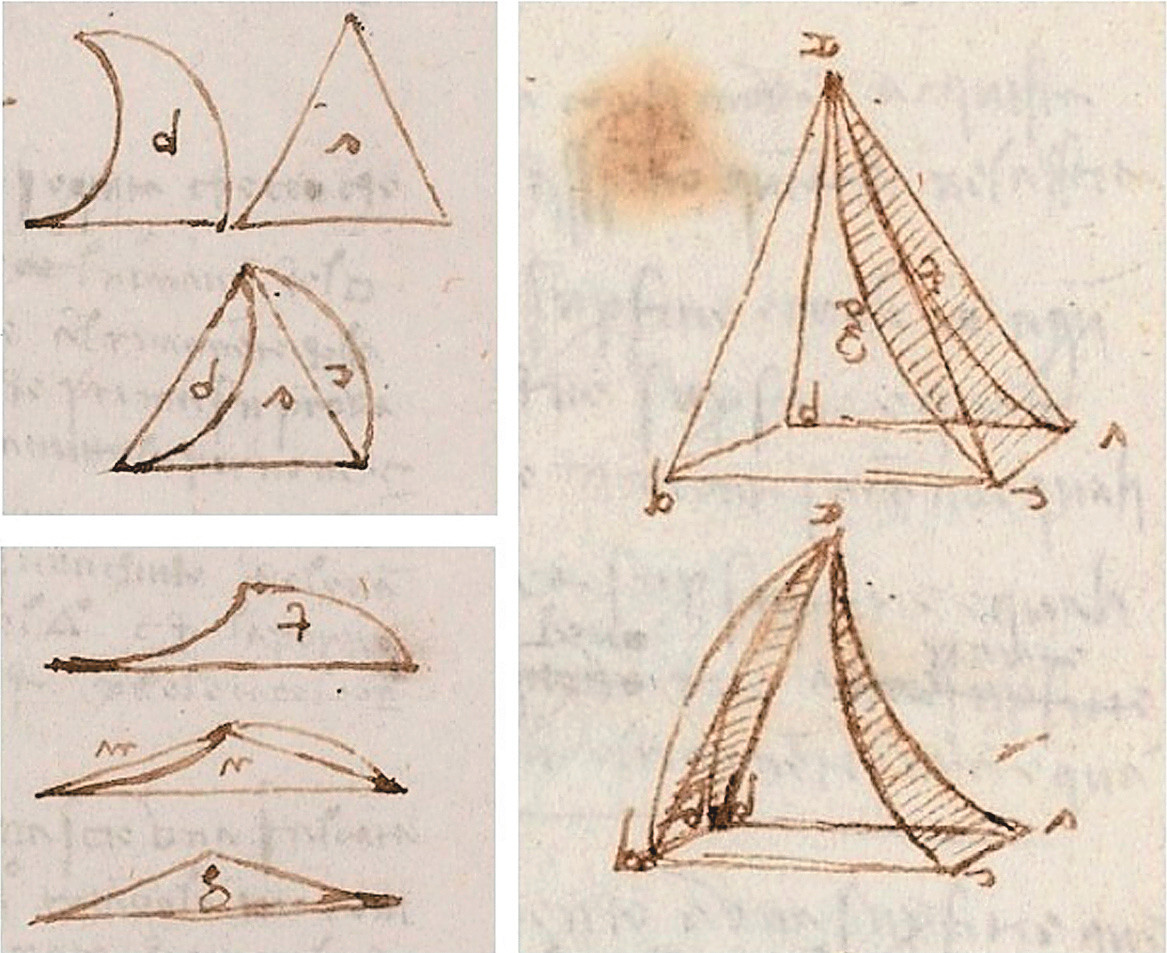
Теорема Гиппократа покорила и вдохновила да Винчи, и тот обобщил её на случай произвольного прямоугольного треугольника. Пятью веками ранее то же самое сделал арабский учёный Ибн аль-Хайсам, более известный европейцам под именем Альхазен, с чьим трактатом «Квадратура круга», где давалось аналогичное его собственному доказательство, Леонардо не был знаком, то есть получил такой же результат независимо от аль-Хайсама. Так что можно записать это, в общем-то, скромное по меркам геометрии достижение и на счёт мастера да Винчи. Правда, на большее в то время рассчитывать было нельзя. Впоследствии теорией круговых луночек занимались Франсуа Виет, Даниил Бернулли, Леонард Эйлер и другие известные и не очень математики. В XVIII столетии задача Гиппократа из числа конструктивных перешла в разряд алгебраических, тогда же были найдены ещё две квадрируемых луночки. Среди всех знаменитых задач древности, включая квадратуру круга, именно она оказалась самой неприступной крепостью, ибо продержалась дольше всех. Точка в истории её покорения была поставлена лишь в середине XX века, когда наконец удалось доказать: существует только пять видов квадрируемых круговых луночек.
Геометрия, доказываемая движением
Одними только построениями дело не ограничилось. Леонардо рассматривает также равносоставленные фигуры и пользуется тем, что они равновелики. При этом действует в духе Евклида, по учебнику которого постигал геометрию: оперирует самими площадями, а не числами, что их выражают, представляя площадь как часть плоскости, заключённую в данной фигуре. Само преобразование сводится к перекраиванию исходной фигуры — разрезанию её на конечное число частей и составлению из них новой фигуры. Ясно, что от простой перестановки фрагментов их суммарная площадь не изменится. Геометры прежних веков применяли указанный приём, имея дело с многоугольниками: при доказательстве теоремы Пифагора, в задачах на деление площадей прямыми линиями и пр. С той же целью к нему прибегали и математики эпохи Возрождения.
А вот Леонардо пошёл дальше и приспособил этот приём к криволинейным фигурам. Вот простой, но показательный пример. Обычный треугольник он преобразует в криволинейный, отрезая с одной стороны фигуры сегмент и приставляя его к другой стороне. Как решить задачу технически — это уже другой вопрос, тут важна сама идея. Ничто не мешает проделать то же самое с квадратом. И вот уже среди рисунков мастера появляются... криволинейные «пифагоровы штаны», этакое обобщение знаменитой теоремы в стиле да Винчи. Серия эскизов позволяет даже проследить их «эволюцию». Точно так же, перейдя от плоских фигур к объёмным, он будет пробовать перекроить многогранники. Да, геометрия Леонардо — во многом эмпирическая наука, а сам он в первую очередь практик и экспериментатор; зачастую поиск решения и конечный результат занимают его больше всего.
