Необычный резонансный преобразователь напряжения

“Чудеса” резонанса

Владимир Уткин

В отличие от классических резонансных преобразователей напряжения, где используется один резонансный контур и понижающий или повышающий трансформатор (в зависимости от назначения преобразователя), в статье рассматривается резонансный преобразователь напряжения на основе пары связанных резонансных контуров (без дополнительного понижающего или повышающего трансформатора). Такой подход приводит к возникновению ряда парадоксов.

Основной парадокс данного резонансного преобразователя заключается в том, что для повышения напряжения в N раз соотношение витков в контурах должно образовывать понижающий напряжение в N раз трансформатор. А для понижения напряжения в N раз соотношение витков в контурах должно образовывать повышающий напряжение в N раз трансформатор. Вот такое «нарушение» здравого смысла.

Более того, данный преобразователь может быть построен для случая, когда число витков в контурах совпадает. В этом случае выходное напряжение определяется соотношением емкостей конденсаторов, подключенных к первичному и вторичному контуру. Для повышения напряжения в N раз емкость конденсатора вторичного контура должна быть в N раз меньше емкости конденсатора первичного контура. Для понижения напряжения – наоборот. Структурная схема такого варианта представлена ниже на рис. 1.

Рис. 1. Структурная схема резонансного преобразователя напряжения на основе пары связанных резонансных контуров при равном числе витков в контурах, где Ꞷ2 – резонансная частота связанных контуров

Следовательно, чтобы повысить или понизить напряжение, достаточно изменять соотношение емкостей конденсаторов в контурах без изменения числа витков в контурах. Никакой дополнительный повышающий или понижающий трансформатор не потребуется.

Идея такого парадоксального преобразователя напряжения основана на теории связанных резонансных контуров. Эту теорию можно подробно изучить по учебнику, указанному в конце статьи, либо в Интернете по запросу: «Связанные резонансные контуры».

Из теории известно, что при коэффициенте связи контуров К > 0,7 их резонансная кривая приобретает «двугорбый» вид с резонансами на частотах Ꞷ1 и Ꞷ2, показанный на рис. 2. Чем больше коэффициент связи контуров К, тем больше отличаются резонансные частоты Ꞷ1 и Ꞷ2, которые определяются по следующим формулам.

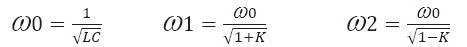
Происходит это за счет того, что фаза колебаний во вторичном контуре на частоте Ꞷ2 отличается на 180 градусов от фазы колебаний в первичном контуре. В результате электромагнитные поля катушек контуров направлены встречно и подавляют друг друга. Откуда следует, что чем ближе катушки друг к другу (больше коэффициент связи К), тем сильнее подавление и выше резонансная частота Ꞷ2 за счет уменьшения эффективной индуктивности катушек.

Рис. 2. Резонансные кривые связанных резонансных контуров в зависимости от коэффициента связи К

При этом в литературе рассматривается вариант связанных резонансных контуров, когда они идентичны. То есть совпадают индуктивности и емкости первого и второго контура.

В то же время резонансы будут наблюдаться даже тогда, когда параметры первого и второго контура не совпадают. Правда, на других частотах – Ꞷ1 и Ꞷ2, но все равно будут наблюдаться. И вот здесь происходит самое интересное с точки зрения преобразования напряжения. Напряжение на выходном контуре будет зависеть от соотношения резонансных частот контуров, на которые они первоначально настроены. Чем выше резонансная частота выходного контура по отношению к входному контуру, тем выше напряжение на выходе. И наоборот. Обобщенные графики этой зависимости представлены на рис. 3 для случаев (А) и (В).

Рис. 3. Зависимость резонансной частоты Ꞷ2 и напряжения U2 на выходном контуре от соотношения числа витков контуров (А), и соотношения емкостей конденсаторов С2/С1 при равном числе витков контуров (В)

Эти зависимости и лежат в основе резонансных преобразователей, обладающих необычными, парадоксальными свойствами.